sm 기술 블로그
103. 1004(어린 왕자) 본문
import java.util.*;
import java.io.*;
class Main{
public static void main(String args[])throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringBuilder sb = new StringBuilder();
int T = Integer.parseInt(br.readLine());
for(int i = 0; i < T; i++) {
String[] sBits = br.readLine().split(" ");
int x1 = Integer.parseInt(sBits[0]);
int y1 = Integer.parseInt(sBits[1]);
int x2 = Integer.parseInt(sBits[2]);
int y2 = Integer.parseInt(sBits[3]);
int cnt = 0;
int N = Integer.parseInt(br.readLine());
for(int j =0; j < N; j++) {
String[] sBits2 =br.readLine().split(" ");
int cx = Integer.parseInt(sBits2[0]);
int cy = Integer.parseInt(sBits2[1]);
int r = Integer.parseInt(sBits2[2]);
double d1 = Math.pow(Math.pow(x1-cx, 2) + Math.pow(y1-cy, 2),0.5);
double d2 = Math.pow(Math.pow(x2-cx, 2) + Math.pow(y2-cy, 2),0.5);
if((d1 > r && d2 < r) || (d1 < r && d2 > r)) {
cnt++;
}
}
sb.append(cnt).append("\n");
}
System.out.print(sb);
}
}문제요약
출발점과 도착점이 있는데 원을 진입,이탈하는 수를 구하라.
설명

다음과 같이 빨간선이 경로이고 빨간점이 출발점과 도착점이다.
원의 거리는

다음과 같이 구할 수 있다.
이 거리가 r보다 작으면 진입 크면 이탈한 것이다.
도착점, 출발점이 주어지는 원 안에 둘다 속하거나 둘다 속하지 않으면 진입이나 이탈이 발생하지 않는다.
즉, 도착점이 r보다 작아서 진입해야하고, 출발점이 r보다 커서 이탈해야 한다면 진입|이탈이 발생한 것이다.
혹은 도착점이 r보다 커서 이탈해야하고, 출발점이 r보다 작아서 진입해야한다.
예를 들어 12 1 2 와 2 2 2 일때, 시작점과 출발점이 -5 1 12 1 인 경우를 보자
12 1 2는


이다.
d1이 r보다 크고, d2가 r보다 작아서 진입|이탈이 발생한 경우이다.
2 2 2는
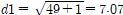

이다.
r이 d1과 d2보다 작기 때문에 진입|이탈이 발생하지 않는다.


진입,이탈이 발생하지 않는 경우는 점과 원이 아닌 두원이라 했을 때 위와 같다고 볼 수 있다.
마지막으로 최종으로 정리하면

다음과 같이 하나의 점의 거리는 반지름 보다 작고, 나머지 하나의 점의 거리가 반지름 보다 크다면 이탈 | 진입이 발생하고,


다음과 같이 d1,d2가 반지름의 길이보다 작고, 혹은 클 때는 진입|이탈이 발생하지 않는다.
'문제 > 백준_자바' 카테고리의 다른 글
| 105. 5086(배수와 약수) (0) | 2022.06.24 |
|---|---|
| 104. 1358(하키) (0) | 2022.06.23 |
| 102. 1002(터렛) (0) | 2022.06.22 |
| 101. 택시 기하학(3053) (0) | 2022.06.22 |
| 100. 2477(참외 밭) (0) | 2022.06.22 |
Comments



