sm 기술 블로그
171. 10830(피보나치 수 6) - 파이썬 본문
import sys
input = sys.stdin.readline
n = int(input())
p = 1000000007
def MatrixMul(A, B):
l = len(A)
C = [[0]*l for _ in range(l)]
for i in range(l):
for j in range(l):
for k in range(l):
C[i][j] += A[i][k] * B[k][j]
remainder(C)
return C
def remainder(A):
l = len(A)
for i in range(l):
for j in range(l):
A[i][j] %= p
def pow(A, B):
if B == 1:
remainder(A)
return A
tmp = pow(A, B//2)
if B % 2 == 1:
return MatrixMul(MatrixMul(tmp, tmp), A)
else:
return MatrixMul(tmp, tmp)
print(pow([[1, 1], [1, 0]], n)[0][1])문제요약
피보나치 수열을 구하라 (분할정복을 이용해서)
설명
이 문제의 핵심은 행렬의 거듭제곱을 통해서 피보나치 수열을 구할 수 있다는 것이다.
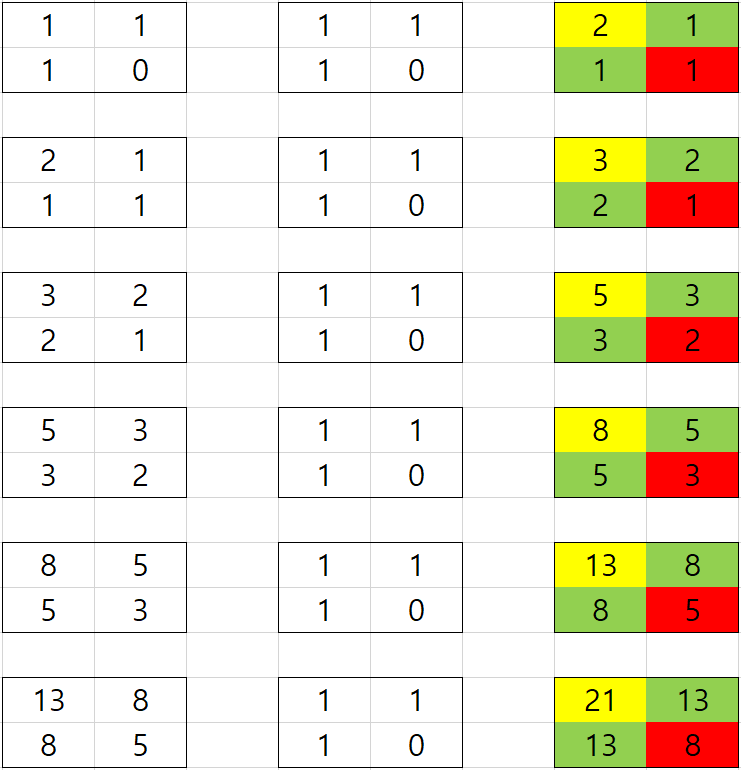
위 식을 보면 규칙이 보일 것이다.

이 놈의 거듭제곱의 형태의 [0 , 0]이, [0 , 1]과 [1 , 0]이, [1 , 1]이 피보나치 수열을 이루고 있다.
우리는 0, 1, 1, 2, 3, 5 ... 식으로 피보나치 수열을 구한다.
따라서 [0, 1]과 [1, 0] 번째가 본래 처음부터의 피보나치 수열을 나타낸다.
결과적으로 점화식은 다음과 같을 것이다.

각 코드의 상세정보는
https://smhope.tistory.com/449?category=1058420
170. 10830(행렬 제곱) - 파이썬
import sys input = sys.stdin.readline # 행렬 곱을 처리하는 부분 def MatrixMul(A, B): N = len(A) C = [[0 for _ in range(N)] for _ in range(N)] for i in range(N): for j in range(N): for k in range(N):..
smhope.tistory.com
를 참고하면 된다.
'문제 > 백준_파이썬' 카테고리의 다른 글
| 173. 3003(킹, 퀸, 룩, 비숍, 나이트, 폰) - 파이썬 (0) | 2022.08.13 |
|---|---|
| 172. 6549 (히스토그램에서 가장 큰 직사각형) - 파이썬 (0) | 2022.08.06 |
| 170. 10830(행렬 제곱) - 파이썬 (0) | 2022.08.04 |
| 169. 2740(행렬곱셈) - 파이썬 (0) | 2022.08.02 |
| 168. 1629(이항계수3) - 파이썬 (0) | 2022.08.01 |
Comments



