sm 기술 블로그
168. 1629(이항계수3) - 파이썬 본문
import sys
input = sys.stdin.readline
N, K = map(int, input().split())
P = 1000000007
def pow(base, expo):
if expo == 0:
return 1
tmp = pow(base, expo // 2)
if expo % 2 == 1:
return (tmp * tmp % P) * base % P
else:
return tmp * tmp % P
def factorial(N):
f = 1
while (N > 1):
f = (f * N) % P
N -= 1
return f
# A는 분자 B는 분모
# 분자 N!
A = factorial(N)
# 분모 (K! * (N-K)!) mod p
B = factorial(K) * factorial(N-K) % 1000000007
# 페르마의 정리 이용
print(A * pow(B, 1000000007-2) % P)문제요약
숫자가 매우 큰 이항계수 정리를 진행하라.
설명
이번 문제 역시 수가 매우크기 때문에 그냥 이항계수 정리를 진행하면 시간초과가 발생할 수 밖에 없다.
여기서는 페르마의 정리가 이용된다.
페르마의 정리란 아래와 같다.

정리하면 나눠지지 않는 수 즉 a가 p의 배수가 아닐때 다음과 같은 식으로 나타낼 수 있다는 것이다.


이항정리는 위와같은 식이므로 페르마의 정리를 이용하면

다음과 같이 구할 수 있다.
위식이 2번과 같이 될 수 있는 이유는 곱셈 분배법칙에 의한 것이다.

(K! (N-K)!)1000000007-2식이 왜 나왔는지 궁금할 수 있다.
이식은 역원에 대한 식이다.
즉, a (mod p) 에 대한 역원은 ap-2 (mod p)

먼저 (K! (N-K)!)1000000007-2은 거듭제곱과 같은 것으로 우리는 https://smhope.tistory.com/441 에서 아래의 메소드를 이용해서 풀었다.
def pow(base, expo):
if expo == 0:
return 1
tmp = pow(base, expo // 2)
if expo % 2 == 1:
return (tmp * tmp % P) * base % P
else:
return tmp * tmp % P그리고 팩토리얼을 사용했다. 팩토리얼은 재귀함수를 사용하면 다음과 같은 메소드로 나타낼 수 있다.
def factorial(N):
f = 1
while (N > 1):
f = (f * N) % P
N -= 1
return f메소드를 정의했으면 하나하나 풀면된다.

먼저 우리가 최종적으로 구해야 하는 식이다.
이 식을 파이썬을 이용해서 만들어 보면,
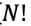
# 분자 N!
A = factorial(N)
# 분모 (K! * (N-K)!) mod p
B = factorial(K) * factorial(N-K) % 1000000007결국
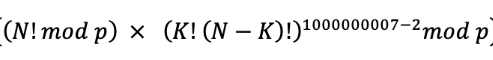
이 부분이
A * pow(B, 1000000007-2)이 부분으로 된다.
최종적으로는
print(A * pow(B, 1000000007-2) % P)이 식이 위와 같게 된다.
'문제 > 백준_파이썬' 카테고리의 다른 글
| 170. 10830(행렬 제곱) - 파이썬 (0) | 2022.08.04 |
|---|---|
| 169. 2740(행렬곱셈) - 파이썬 (0) | 2022.08.02 |
| 167. 1629(곱셈) - 파이썬 (0) | 2022.07.31 |
| 166. 1780(종이의 개수) - 파이썬 (0) | 2022.07.31 |
| 165. 1992(쿼드트리) - 파이썬 (0) | 2022.07.30 |
Comments




