sm 기술 블로그
133. 1463(1로 만들기) 본문
N = int(input())
dp = [-1] * (10**6+1)
dp[1] = 0
dp[2] = 1
dp[3] = 1
if N > 3:
for i in range(4, N+1): #-1씩 해도 최대 N번임
dp[i] = dp[i-1]+1
if i % 3 == 0:
dp[i] = min(dp[i], dp[i//3]+1)
if i % 2 == 0:
dp[i] = min(dp[i], dp[i//2]+1)
print(dp[N])문제요약
조건 1: 3으로 나눠지면 3으로 나눈다
조건 2: 2로 나눠지면 2로 나눈다
조건 3: 1을 뺀다.
세가지 조건을 가장 적게 사용해서 1로 만들어라.
설명
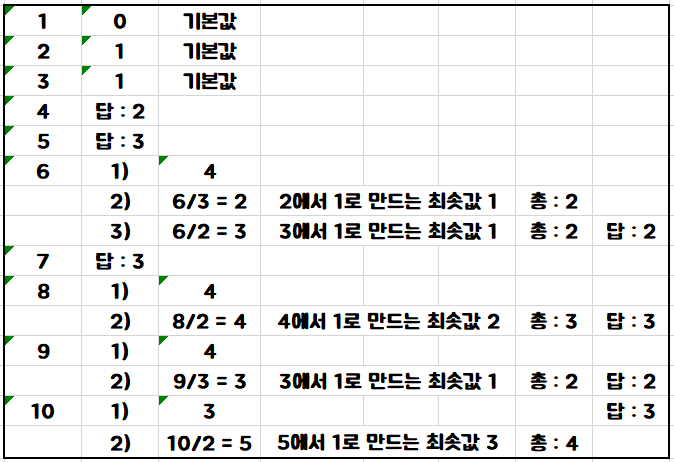
먼저 3까지는 기본값으로 초기화 해준다.
입력값이 6인 경우까지 설명 하겠다.
1. 4인경우
1) 1을 뺏을 경우 -> 4 - 1 = 3
3을 1로 만드는 최소값은 1이다.
따라서 1(1을 빼는 조건 사용) + 1(3을 1로 만드는 최소값) = 2
2) 4를 2로 나눈 경우 -> 4 / 2 = 2
2를 1로 만드는 최소값은 1이다
따라서 1(2로 나누는 조건 사용) + 1(2를 1로 만드는 최소값) = 2
최소값 : 2
2. 5인경우
1) 1을 뺏을 경우 -> 5 - 1 = 4
4를 1로 만드는 값은 2이다.
따라서 1(1을 빼는 조건 사용) + 2(4를 1로 만드는 최소값) = 3
최소값 : 3
3. 6인경우
1) 1을 뺏을 경우 -> 6 - 1 = 5
5를 최소로 만드는 최소값은 3이다.
따라서 1(1을 빼는 조건 사용) + 3(5를 1로 만드는 최소값) = 4
2) 6을 3으로 나눈 경우 -> 6 / 3 = 2
2를 1로 만드는 최소값은 1이다.
따라서 1(3으로 나누는 조건 사용) + 1(2를 1로 만드는 최소값) = 2
3) 6을 2로 나눈 경우 -> 6 / 2 = 3
3을 1로 만드는 최소값은 1이다.
따라서 1(2로 나누는 조건 사용) + 1(3을 1로 만드는 최소값) = 2
최소값 : 2
dp[i] = dp[i-1]+1전 조건에 최소값 + 1 하면 현재 index i의 1을 뺏을 경우 최소로 1로 만드는 경우이다.
if i % 3 == 0:
dp[i] = min(dp[i], dp[i//3]+1)1을 뺏을 경우 1로 만드는 최소값과 3으로 나눴을 때 해당 인덱스의 1로 만드는 최소값 + 1 중 더 작은 값을 저장한다.
if i % 2 == 0:
dp[i] = min(dp[i], dp[i//2]+1)2로 나누어 떨어질 경우이다.
만약 3으로도 나누어 떨어지면, 위에서 조건3과 조건2중 dp[i] 최소값을 저장했다.
따라서 여기서는 조건3과 조건2중 dp[i] 최소값과 2로 나눈 해당 인덱스의 1로 만드는 최소값 + 1 중 더 작은 값을 저장한다.
'문제 > 백준_파이썬' 카테고리의 다른 글
| 136. 11053(가장 긴 증가하는 부분 수열) (0) | 2022.07.08 |
|---|---|
| 135. 2156(포도주 시식) (0) | 2022.07.08 |
| 132. 2579(계단 오르기) (0) | 2022.07.04 |
| 131. 1932(정수 삼각형) (0) | 2022.07.03 |
| 130. 1149(RGB 거리) (0) | 2022.07.03 |



