sm 기술 블로그
정렬 본문
1. 선택 정렬(Selection Sort)
현재 위치에 들어갈 값을 찾아 정렬하는 배열이다.
현재 위치에 저장될 갓의 크기가 작냐, 크냐에 따라 최소 선택 정렬, 최대 선택 정렬로 구분 할 수 있다.
기본 로직
(1) 정렬 되지 않은 인덱스의 맨 앞에서 부터, 이를 포함한 그 이후의 배열값 중 가장 작은 값을 찾아간다.
(2) 가장 작은 값을 찾으면, 그 값을 현재 인덱스의 값과 바꿔준다.
(3) 위 과정을 반복한다.
시간 복잡도 O(N^2)
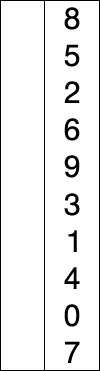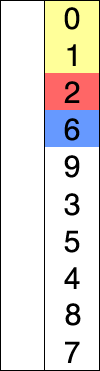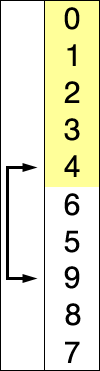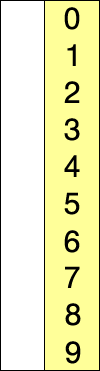
https://www.youtube.com/watch?time_continue=5&v=92BfuxHn2XE&feature=emb_logo
public class Selection_Sort {
public static void selection_sort(int[] a) {
selection_sort(a, a.length);
}
private static void selection_sort(int[] a, int size) {
for(int i = 0; i < size - 1; i++) {
int min_index = i;
// 최솟값을 갖고있는 인덱스 찾기
for(int j = i + 1; j < size; j++) {
if(a[j] < a[min_index]) {
min_index = j;
}
}
// i번째 값과 찾은 최솟값을 서로 교환
swap(a, min_index, i);
}
}
private static void swap(int[] a, int i, int j) {
int temp = a[i];
a[i] = a[j];
a[j] = temp;
}
}
2. 삽입 정렬(Insertion Sort)
현재 위치에서 그 이하의 배열들을 비교하여 자신이 들어갈 위치를 찾아 그 위치에 삽입하는 배열 알고리즘.
기본 로직
(1) 두 번째 인덱스 부터 시작한다. 현재 인덱스는 별도의 변수에 저장해 주고, 비교 인덱스를 현재 인덱스 -1로잡는다.
(2) 별도로 저장해 둔 삽입을 위한 변수와 비교 인덱스의 배열 값을 비교한다.
(3) 삽입 변수의 값이 더 작으면 현재 인덱스로 비교 인덱스의 값을 저장해주고, 비교 인덱스 -1하여 비교를 반복한다.
(4) 만약 삽입 변수가 더 크면, 비교 인덱스 +1에 삽입 변수를 저장한다.
시간 복잡도
역으로 정렬되어 있는 경우 : O(N^2)
이미 정렬되어 있는 경우 : O(N)

https://www.youtube.com/watch?v=8oJS1BMKE64
public class Insertion_Sort {
public static void insertion_sort(int[] a) {
insertion_sort(a, a.length);
}
private static void insertion_sort(int[] a, int size) {
for(int i = 1; i < size; i++) {
// 타겟 넘버
int target = a[i];
int j = i - 1;
// 타겟이 이전 원소보다 크기 전 까지 반복
while(j >= 0 && target < a[j]) {
a[j + 1] = a[j]; // 이전 원소를 한 칸씩 뒤로 미룬다.
j--;
}
/*
* 위 반복문에서 탈출 하는 경우 앞의 원소가 타겟보다 작다는 의미이므로
* 타겟 원소는 j번째 원소 뒤에 와야한다.
* 그러므로 타겟은 j + 1 에 위치하게 된다.
*/
a[j + 1] = target;
}
}
}--->> while(j >= 0 && target < a[j]) 빼놓은 값이 이전 원소보다 크기 전 까지 반복
3. 버블 정렬(Bubble Sort)
연속된 두개 인덱스를 비교하여, 정한 기준의 값을 뒤로 넘겨 정렬하는 방법.
오름차순으로 정렬하고자 할 경우, 비교시마다 큰 값이 뒤로 이동하여, 1바퀴 돌시 가장 큰값이 맨뒤에 저장된다.
맨 마지막에는 비교하는 수들 중 가장 큰값이 저장 되기 때문에, (전체 배열의 크기 - 현재까지 순환한 바퀴수)만큼 반복하면 된다.
기본 로직
(1) 두 번째 인덱스부터 시작한다. 현재 인덱스 값과, 바로 이젖의 인덱스 값을 비교한다.
(2) 만약 이전 인덱스가 더 크면 현재 인덱스와 바꿔 준다.
(3) 현재 인덱스가 더 크면 교환하지 않고 다음 두 연속된 배열값을 비교한다.
(4) 이를 (전체 배열의 크기 - 현재까지 순환한 바퀴 수)만큼 반복한다.
시간 복잡도 O(N^2)
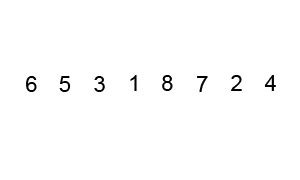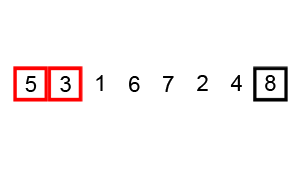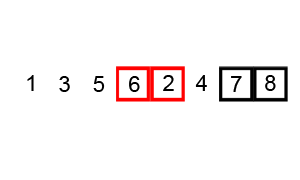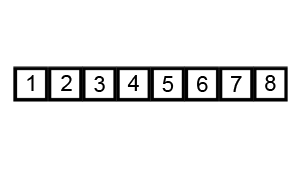
https://www.youtube.com/watch?time_continue=61&v=Cq7SMsQBEUw&feature=emb_logo
public class Bubble_Sort {
public static void bubble_sort(int[] a) {
bubble_sort(a, a.length);
}
private static void bubble_sort(int[] a, int size) {
// round는 배열 크기 - 1 만큼 진행됨
for(int i = 1; i < size; i++) {
// 각 라운드별 비교횟수는 배열 크기의 현재 라운드를 뺀 만큼 비교함
for(int j = 0; j < size - i; j++) {
/*
* 현재 원소가 다음 원소보다 클 경우
* 서로 원소의 위치를 교환한다.
*/
if(a[j] > a [j + 1]) {
swap(a, j, j + 1);
}
}
}
}
private static void swap(int[] a, int i, int j) {
int temp = a[i];
a[i] = a[j];
a[j] = temp;
}
}
4. 합병 정렬(Merge Sort)
분할 정복 방식으로 설계된 알고리즘이다. 분할 정복은 큰 문제를 반으로 쪼개 문제를 해결해 나가는 방식으로, 분할은 배열의 크기가 1보다 작거나 같을 때 까지 반복한다.
입력으로 하나의 배열을 받고, 연산 중에 두개의 배열로 계속 쪼개 나간 뒤, 합치면서 정렬해 최후에는 하나의 정렬을 출력한다.
합병은 두 개의 배열을 비교하여, 기준에 맞는 값을 다른 배열에 저장해 나간다.
분할 과정
(1) 현재 배열을 반으로 쪼갠다. 배열의 시작 위치와 종료위치를 입력받아 둘을 더한 후 2를 나눠 그 위치를 기준으로 나눈다.
(2) 이를 쪼갠 배열의 크기가 0이거나 1일때 까지 반복한다.
합병 과정
(1) 두 배열 A,B의 크기를 비교한다. 각각의 배열의 현재 인덱스를 i, j로 가정한다.
(2) i에는 A 배열의 시작 인덱스를 저장하고 j에는 B 배열의 시작 주소를 저장한다.
(3) A[i] 와 B[j]를 비교한다. 오름차순의 경우 이중에 작은 값을 새 배열 C에 저장한다.
A[i] 가 더 컸다면 A[i]의 값을 배열 C에 저장해주고, i의 값을 하나 증가시켜준다.
(4) 이를 i나 j 둘 중 하나가 각자 배열의 끝에 도달할 때 까지 반복한다.
(5) 끝까지 저장을 못한 배열의 값을, 순서대로 전부 다 C에 저장한다.
(6) C 배열을 원래의 배열에 저장해둔다.
시간 복잡도 O(NlogN)


https://www.youtube.com/watch?time_continue=8&v=ZRPoEKHXTJg&feature=emb_logo
Top-Down 방식
public class Merge_Sort {
private static int[] sorted; // 합치는 과정에서 정렬하여 원소를 담을 임시배열
public static void merge_sort(int[] a) {
sorted = new int[a.length];
merge_sort(a, 0, a.length - 1);
sorted = null;
}
// Top-Down 방식 구현
private static void merge_sort(int[] a, int left, int right) {
/*
* left==right 즉, 부분리스트가 1개의 원소만 갖고있는경우
* 더이상 쪼갤 수 없으므로 return한다.
*/
if(left == right) return;
int mid = (left + right) / 2; // 절반 위치
merge_sort(a, left, mid); // 절반 중 왼쪽 부분리스트(left ~ mid)
merge_sort(a, mid + 1, right); // 절반 중 오른쪽 부분리스트(mid+1 ~ right)
merge(a, left, mid, right); // 병합작업
}
/**
* 합칠 부분리스트는 a배열의 left ~ right 까지이다.
*
* @param a 정렬할 배열
* @param left 배열의 시작점
* @param mid 배열의 중간점
* @param right 배열의 끝 점
*/
private static void merge(int[] a, int left, int mid, int right) {
int l = left; // 왼쪽 부분리스트 시작점
int r = mid + 1; // 오른쪽 부분리스트의 시작점
int idx = left; // 채워넣을 배열의 인덱스
while(l <= mid && r <= right) {
/*
* 왼쪽 부분리스트 l번째 원소가 오른쪽 부분리스트 r번째 원소보다 작거나 같을 경우
* 왼쪽의 l번째 원소를 새 배열에 넣고 l과 idx를 1 증가시킨다.
*/
if(a[l] <= a[r]) {
sorted[idx] = a[l];
idx++;
l++;
}
/*
* 오른쪽 부분리스트 r번째 원소가 왼쪽 부분리스트 l번째 원소보다 작거나 같을 경우
* 오른쪽의 r번째 원소를 새 배열에 넣고 r과 idx를 1 증가시킨다.
*/
else {
sorted[idx] = a[r];
idx++;
r++;
}
}
/*
* 왼쪽 부분리스트가 먼저 모두 새 배열에 채워졌을 경우 (l > mid)
* = 오른쪽 부분리스트 원소가 아직 남아있을 경우
* 오른쪽 부분리스트의 나머지 원소들을 새 배열에 채워준다.
*/
if(l > mid) {
while(r <= right) {
sorted[idx] = a[r];
idx++;
r++;
}
}
/*
* 오른쪽 부분리스트가 먼저 모두 새 배열에 채워졌을 경우 (r > right)
* = 왼쪽 부분리스트 원소가 아직 남아있을 경우
* 왼쪽 부분리스트의 나머지 원소들을 새 배열에 채워준다.
*/
else {
while(l <= mid) {
sorted[idx] = a[l];
idx++;
l++;
}
}
/*
* 정렬된 새 배열을 기존의 배열에 복사하여 옮겨준다.
*/
for(int i = left; i <= right; i++) {
a[i] = sorted[i];
}
}
}Bottom-Up 방식
public class Merge_Sort {
private static int[] sorted; // 합치는 과정에서 정렬하여 원소를 담을 임시배열
public static void merge_sort(int[] a) {
sorted = new int[a.length];
merge_sort(a, 0, a.length - 1);
sorted = null;
}
// Bottom-Up 방식 구현
private static void merge_sort(int[] a, int left, int right) {
for(int size = 1; size <= right; size += size) {
for(int l = 0; l <= right - size; l += (2 * size)) {
int low = l;
int mid = l + size - 1;
int high = Math.min(l + (2 * size) - 1, right);
merge(a, low, mid, high); // 병합작업
}
}
}
/**
* 합칠 부분리스트는 a배열의 left ~ right 까지이다.
*
* @param a 정렬할 배열
* @param left 배열의 시작점
* @param mid 배열의 중간점
* @param right 배열의 끝 점
*/
private static void merge(int[] a, int left, int mid, int right) {
int l = left; // 왼쪽 부분리스트 시작점
int r = mid + 1; // 오른쪽 부분리스트의 시작점
int idx = left; // 채워넣을 배열의 인덱스
while(l <= mid && r <= right) {
if(a[l] <= a[r]) {
sorted[idx] = a[l];
idx++;
l++;
}
else {
sorted[idx] = a[r];
idx++;
r++;
}
}
if(l > mid) {
while(r <= right) {
sorted[idx] = a[r];
idx++;
r++;
}
}
else {
while(l <= mid) {
sorted[idx] = a[l];
idx++;
l++;
}
}
for(int i = left; i <= right; i++) {
a[i] = sorted[i];
}
}
}대부분 정렬 과정은 재귀를 피하는것이 좋기 때문에 Bottom-Up으로 구현하자.
5. 퀵 정렬(Quick Sort)
기준이 되는 값을 하나 설정하여, 그 값을 기준으로 작은 값은 왼쪽으로, 큰값은 오른쪽으로 옮기는 방식으로 정렬한다.
기본로직
(1) point로 잡을 배열의 값 하나를 정한다. 보통 맨 앞이나 맨 뒤, 혹은 전체 배열 값 중의 중간값이나 랜덤 갓으로 정한다.
(2) 분할을 진행하기에 앞서, 비교를 진행하기 위해 가장 왼쪽 배열의 인덱스를 저장하는 left 변수, 가장 오른쪽 배열의 인덱스를 저장한
right변수를 생성한다.
(3) right부터 비교를 진행한다. 비교는 right가 left보다 클 때만 반복하며, 비교한 배열값이 point보다 크면 right를 하나 감소시키고 비교 를 반복한다. point 보다 작은 배열 값을 찾으면 반복을 중지한다.
(4) 그 다음 left부터 비교를 진행한다. 비교는 right가 left보다 클 때만 반복하며. 비교한 배열값이 point보다 작으면 left를 하나 증가시키 고 비교를 반복한다. point보다 큰 배열 값을 찾으면 반복을 중지한다.
(5) left 인덱스의 값과 right 인덱스의 값을 바꿔준다.
(6) 3,4,5 과정을 left < right가 만족 할 때 까지 반복한다.
(7) 위 과정이 끝나면 left의 값과 point를 바꿔준다.
(8) 맨 왼쪽부터 left -1 까지, left +1 부터 맨 오른쪽까지로 나눠 퀵 정렬을 반복한다.
시간 복잡도 O(NlogN) [최악의 경우 O(N^2)]

https://www.youtube.com/watch?v=8hEyhs3OV1w&t=1s
public class QuickSort {
public static void sort(int[] a) {
m_pivot_sort(a, 0, a.length - 1);
}
/* 중간 피벗 선택 방식
* @param a 정렬할 배열
* @param lo 현재 부분배열의 왼쪽
* @param hi 현재 부분배열의 오른쪽
*/
private static void m_pivot_sort(int[] a, int lo, int hi) {
if(lo >= hi) {
return;
}
int pivot = partition(a, lo, hi);
m_pivot_sort(a, lo, pivot);
m_pivot_sort(a, pivot + 1, hi);
}
private static int partition(int[] a, int left, int right) {
// lo와 hi는 각각 배열의 끝에서 1 벗어난 위치부터 시작한다.
int lo = left - 1;
int hi = right + 1;
int pivot = a[(left + right) / 2]; // 부분리스트의 중간 요소를 피벗으로 설정
while(true) {
do {
lo++;
} while(a[lo] < pivot);
hi--;
} while(a[hi] > pivot && lo <= hi);
if(lo >= hi) {
return hi;
}
swap(a, lo, hi);
}
}
private static void swap(int[] a, int i, int j) {
int temp = a[i];
a[i] = a[j];
a[j] = temp;
}
}6. 쉘 정렬(Shell Sort)
삽입 정렬 기반으로 간격을 설정하고 그 간격을 줄여나가며 정렬하는 방법
예를 들어
정렬하고자 하는 원소가 10개가 있을 때 간격을 3으로 설정하여 간격이 4인 원소들끼리 삽입정렬을 하고 그 다음 간격을 2로 조정하여 2칸씩 떨어진 원소들끼리 삽입정렬을 하고, 최종적으로 간격이 1인 즉, 우리가 알고있는 기본적인 삽입정렬을 하는 것이다. 이러한 과정을 거치는 것이 바로 셸 정렬이라는 것이다.
기본 로직
(1) 간격(gap)을 설정한다.
(2) 각 간격별로 분류 된 서브(부분) 리스트에 대해 삽입정렬을 한다.
(3) 각 서브(부분) 리스트의 정렬이 끝나면 간격을 줄인다.
(4) 간격이 1이 될 때 까지 2번 과정으로 되돌아가며 반복한다.


https://www.youtube.com/watch?v=n4sk-SzGvZA&t=27s
7. 힙 정렬(Heap Sort)
힙 정렬은 힙 자료구조를 기반으로 하므로 힙 자료구조를 먼저 학습하자.
https://st-lab.tistory.com/205
자바 [JAVA] - 배열을 이용한 Heap (힙) 구현하기
자료구조 관련 목록 링크 펼치기 더보기 0. 자바 컬렉션 프레임워크 (Java Collections Framework) 1. 리스트 인터페이스 (List Interface) 2. 어레이리스트 (ArrayList) 3. 단일 연결리스트 (Singly Li..
st-lab.tistory.com
간단하게 힙은 최솟값 또는 최댓값을 빠르게 찾아내기 위해 완전이진트리 형태로 만들어진 자료구조.
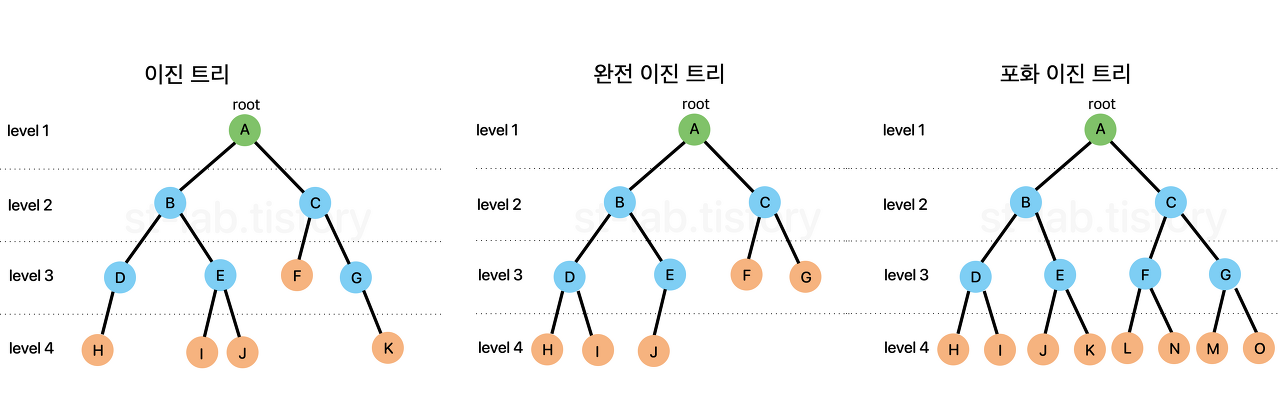

위 구조를 표현하기 위해 배열을 사용하면,

다음과 같다.
위에서 규칙을 보면
[성질]
1. 왼쪽 자식 노드 인덱스 = 부모 노드 인덱스 × 2 + 1
2. 오른쪽 자식 노드 인덱스 = 부모 노드 인덱스 × 2 + 2
3. 부모 노드 인덱스 = (자식 노드 인덱스 - 1) / 2
시간 복잡도 O(NlogN)

https://www.youtube.com/watch?v=_bkow6IykGM&t=40s
public class HeapSort {
public static void sort(int[] a) {
sort(a, a.length);
}
private static void sort(int[] a, int size) {
if(size < 2) {
return;
}
/*
* left child node = index * 2 + 1
* right child node = index * 2 + 2
* parent node = (index - 1) / 2
*/
// 가장 마지막 요소의 부모 인덱스
int parentIdx = getParent(size - 1);
// max heap
for(int i = parentIdx; i >= 0; i--) {
heapify(a, i, size - 1);
}
for(int i = size - 1; i > 0; i--) {
swap(a, 0, i);
heapify(a, 0, i - 1);
}
}
// 부모 인덱스를 얻는 함수
private static int getParent(int child) {
return (child - 1) / 2;
}
// 두 인덱스의 원소를 교환하는 함수
private static void swap(int[] a, int i, int j) {
int temp = a[i];
a[i] = a[j];
a[j] = temp;
}
private static void heapify(int[] a, int parentIdx, int lastIdx) {
int leftChildIdx;
int rightChildIdx;
int largestIdx;
while((parentIdx * 2) + 1 <= lastIdx) {
leftChildIdx = (parentIdx * 2) + 1;
rightChildIdx = (parentIdx * 2) + 2;
largestIdx = parentIdx;
if (a[leftChildIdx] > a[largestIdx]) {
largestIdx = leftChildIdx;
}
if (rightChildIdx <= lastIdx && a[rightChildIdx] > a[largestIdx]) {
largestIdx = rightChildIdx;
}
if (largestIdx != parentIdx) {
swap(a, parentIdx, largestIdx);
parentIdx = largestIdx;
}
else {
return;
}
}
}
}8. 이진 삽입 정렬(Binary Insertion Sort)
삽입 정렬의 메커니즘은 같으나, 원소가 들어 갈 위치를 선형 탐색이 아닌 이분 탐색(이진 탐색)을 이용한 방법으로 구현한다.
기본로직
(1) 현재 타겟이 되는 숫자에 대해 이전 위치에 있는 원소들에 들어 갈 위치를 이분 탐색을 통해 얻어낸다.
(첫 번째 타겟은 두 번째 부터 시작)
(2) 들어가야 할 위치를 비우기 위해 후방 원소들을 한칸 씩 밀고 비운 공간에 타겟을 삽입한다.
(3) 그 다음 타겟을 찾아 위와 같은 방법으로 반복한다.
시간 복잡도
최선 : O(N)
최악 : O(N^2)


public class BinaryInsertionSort {
public static void binaryInsertionSort(int[] a) {
binaryInsertionSort(a, a.length);
}
private static void binaryInsertionSort(int[] a, int size) {
for(int i = 1; i < size; i++) {
// 타겟 넘버
int target = a[i];
// 이분탐색을 통해 target이 들어가야 할 위치를 얻는다.
int location = binarySearch(a, target, 0, i);
int j = i - 1;
// 시프팅 작업
while(j >= location) {
a[j + 1] = a[j]; // 이전 원소를 한 칸씩 뒤로 미룬다.
j--;
}
a[location] = target;
}
}
// 이분 탐색
private static int binarySearch(int[] a, int key, int lo, int hi) {
int mid;
while(lo < hi) {
// 좀 더 빠르게 하기 위해서 /2 대신 >>> 1을 사용해도 된다.
mid = lo + ((hi - lo) / 2);
if(key < a[mid]) {
hi = mid;
}
else {
lo = mid + 1;
}
}
return hi;
}
}9. 팀 정렬(Tim Sort)
합병정렬을 기반으로 구현하되, 일정 크기 이하의 부분 리스크에 대해서는 이진 삽입 정렬을 수행하는 것
전체적인 맥락은 이렇다.
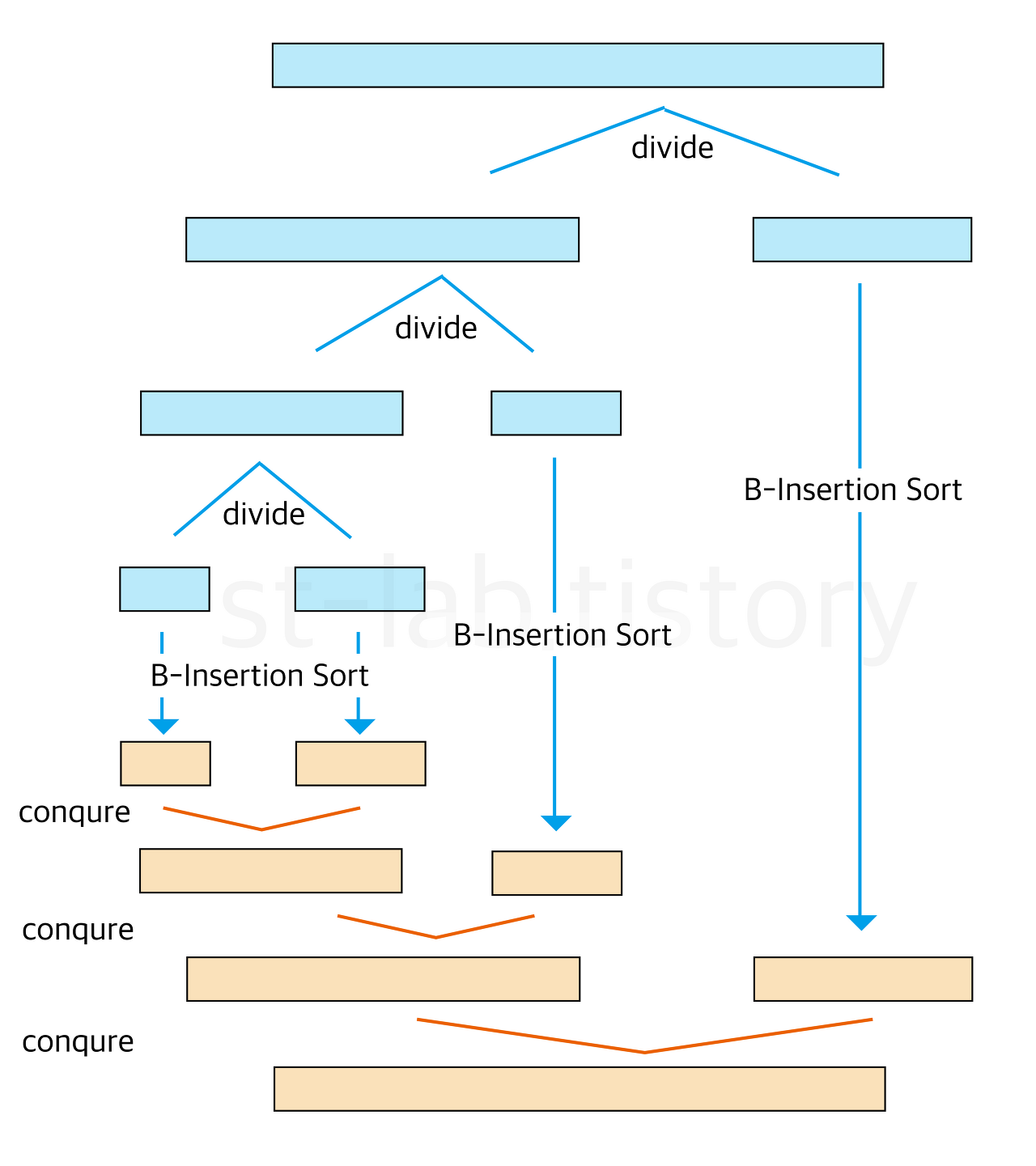
시간 복잡도
최선 : O(N)
최악 : O(NlogN)
코드가 비현실적으로 길다..... 한번 따라 써보고 이해해보자... 너무 어렵다..
public class TimSort {
private static final int THRESHOLD = 32;
/**
* 최소 길이의 run 크기, 즉 minRun을 구하기 위한 메소드
*
* @param runSize minRun을 구하고자 하는 초기 배열의 길이
*/
public static int minRunLength(int runSize) {
int r = 0; // 홀 수가 발생할 때 2^x가 초과되지 않도록 하는 여분의 수
/*
* (runSize & 1) 을 하면, runSize의 가장 오른쪽 비트가 1일 경우에는
* 홀수이므로 1이 반환 될 것이고, r = r | (runSize & 1) 에서 r은 1로 될 것이다.
* 한 번 r이 1로 되면 OR 연산자의 특성상 이 값은 바뀌지 않는다.
*/
while(runSize >= THRESHOLD) {
r |= (runSize & 1);
runSize >>= 1;
}
return runSize + r;
}
// run을 스택에 담아 둘 내부 정적 클래스
private static class IntMergeStack {
private int[] array;
private int[] runBase;
private int[] runLength;
private int stackSize = 0; // run 스택의 원소 개수를 가리킬 변수
public IntMergeStack(int[] a) {
this.array = a;
int len = a.length;
runBase = new int[40];
runLength = new int[40];
}
public void pushRun(int runBase, int runLen) {
this.runBase[stackSize] = runBase;
this.runLength[stackSize] = runLen;
stackSize++;
}
public void mergeForce() {
// 나머지 모든 run을 병합한다.
while (stackSize > 1) {
// 모든 run을 병합 할 것이기 때문에 2번 조건인 runLen[i - 2] > runLen[i - 1] 만 체크해주면서 병합한다.
if (stackSize > 2 && runLength[stackSize - 3] < runLength[stackSize - 1]) {
merge(stackSize - 3);
} else {
merge(stackSize - 2);
}
}
}
public void merge() {
/*
기본 적인 메커니즘
1. runLen[i - 3] > runLen[i - 2] + runLen[i - 1]
2. runLen[i - 2] > runLen[i - 1]
스택에 요소가 5개 있을 때 기본 pivot은 상위 3개 요소 중 가운데를 지정
ex) A, B, C, D, E (A = Bottom, E = Top)
pivot = D (== stackSize - 2)
runLen[pivot - 1] = C, runLen[pivot] = D, runLen[pivot + 1] = E를 스택의 상위 세 요소로 한다.
메커니즘상 루프는 다음과 같은 경우에 기초한다.
1. C <= D + E 및 C < E일 경우 C 과 D 병합. 즉, pivot - 1 과 pivot 병합
2. C <= D + E 및 C >= E일 경우, D와 E 병합. 즉, pivot 과 pivot + 1 병합
3. C > D + E 및 D <= E일 경우, D와 E 병합. 즉, pivot 과 pivot + 1 병합
4. C > D + E 및 D > E일 경우 루프 종료
while (stackSize > 1) {
// 1번 조건 C > B + A 에 위배 될 경우 (== C <= B + A 일 경우)
if (stackSize > 2 && runLength[stackSize - 3] <= runLength[stackSize - 2] + runLength[stackSize - 1] {
// C < A가 크다면 (B, C)를 병합
if (runLength[stackSize - 3] < runLength[stackSize - 1]) {
merge(stackSize - 3);
}
else { // A, B 병합
merge(stackSize - 2);
}
}
// 2번 조건 B > A 에 위배 될 경우 (== B <= A 일 경우)
else if (runLength[stackSize - 2] <= runLength[stackSize - 1]) {
merge(stackSize - 2); // A, B 병합
}
// 그 외의 경우는 위 두 조건을 만족한다는 의미이므로 종료
else {
break;
}
}
위 방식을 그대로 조건식으로 구현할 경우 stack 규칙이 깨짐
예로들어 120, 80, 25, 20이 스택에 있고, 30이 스택에 추가되었다고 가정.
즉, stack[] = {120, 80, 25, 20, 30}
첫 번째 반복문에서 첫 번째 merge() 시
첫 번째 조건문의 runLen[pivot − 1] <= runLen[pivot] + runLen[pivot + 1])
즉, 25 <= (20 + 30) 을 만족시키며, 해당 하위 조건문 runLen[pivot − 1] < runLen[pivot + 1] 인
25 < 30 도 만족시키기 때문에 25와 20이 병합된다.
그러면 결과는, {120, 80, 45, 30} 이 된다.
다음 반복문으로 넘어가게 되면 다음과 같이 된다.
80 > 45 + 30 이기 때문에 첫 번째 조건문을 만족하지 못하며,
그 다음 조건문인 runLen[pivot] <= runLen[pivot + 1] 또한 45 > 30이라
stack의 유지의 두 조건을 모두 만족한다는 의미로 반복문이 종료된다.
하지만, 전체 남아있는 스택을 볼 때, 120 <= 80 + 45 을 만족하는게 있음에도 merge되지 않기에
stack의 규칙이 깨지게 된다.
즉, 상위 3개만 아니라 그 다음 아래의 3개의 요소에 대해서도 검사를 해야한다.
*/
while (stackSize > 1) {
/*
* 1번 조건 C > B + A 에 위배 될 경우 (== C <= B + A 일 경우)
* 혹은, D > C + B 에 위배 될 경우 (== D <= C + B 일 경우)
*/
if (stackSize > 2 && runLength[stackSize - 3] <= runLength[stackSize - 2] + runLength[stackSize - 1]
|| stackSize > 3 && runLength[stackSize - 4] <= runLength[stackSize - 3] + runLength[stackSize - 2]) {
if (runLength[stackSize - 3] < runLength[stackSize - 1]) {
merge(stackSize - 3);
}
else {
merge(stackSize - 2);
}
}
// 2번 조건 B > A 에 위배 될 경우 (== B <= A 일 경우)
else if (runLength[stackSize - 2] <= runLength[stackSize - 1]) {
merge(stackSize - 2);
}
// 그 외의 경우는 위 두 조건을 만족한다는 의미이므로 종료
else {
break;
}
}
}
/**
* run[idx] 와 run[idx + 1]이 병합 됨
*
* @param idx 병합되는 두 서브리스트(run) 중 낮은 인덱스
*/
private void merge(int idx) {
int start1 = runBase[idx];
int length1 = runLength[idx];
int start2 = runBase[idx + 1];
int length2 = runLength[idx + 1];
// idx 와 idx + 1 번째 run을 병합
runLength[idx] = length1 + length2;
/*
* 상위 3개 (A, B, C)에서 A, B가 병합 할 경우 C를 당겨온다.
*
* ex)
* stack [[A], [B], [C]]
*
* runLen[idx] = length1 + length2
* stack[[A + B], [B], [C]]
*
* C를 B위치로 당겨온다.
* stack[[A + B], [C], [C]]
*
* 이 때 마지막 [C](stack[i - 1])는 어차피 더이상 참조될 일 없음
*/
if (idx == (stackSize - 3)) {
runBase[idx + 1] = runBase[idx + 2];
runLength[idx + 1] = runLength[idx + 2];
}
stackSize--;
/*
gallopRight -> <- gallopLeft
RUN A RUN B
______________________________ ______________________________
[ | | || | | |MAX] [MIN| | | | || | ]
------------------------------ ------------------------------
|___________| |______________| |___________________| |______|
less than MIN RUN A' RUN B' greater than MAX
|____________________________________|
merge RUN A' and RUN B'
*/
// start point (RUN B의 시작점보다 작으면서 RUN A 에서 merge를 시작할 위치)
int lo = gallopRight(array[start2], array, start1, length1);
/*
* 만약 RUN A의 길이와 merge를 시작할 지점이 같을 경우
* 이미 정렬되어있는 상태로 정렳 할 필요 없음
*/
if (length1 == lo) {
return;
}
start1 += lo;
length1 -= lo;
// end point (RUN A의 끝 점보다 크면서 RUN B에서 merge가 끝나는 위치)
int hi = gallopLeft(array[start1 + length1 - 1], array, start2, length2);
if (hi == 0) {
return;
}
length2 = hi;
if (length1 <= length2) {
mergeLo(start1, length1, start2, length2);
}
else {
mergeHi(start1, length1, start2, length2);
}
}
/**
* gallop_right() 함수를 수행하여 RUN B 의 첫번째 원소보다
* 큰 원소들이 첫번째 출현하는 위치를 RUN A 에서 찾는다.
*
*
* @param key run B의 key
* @param array 배열
* @param base run A의 시작지점
* @param lenOfA run A 의 길이
* @return 제외되어야 할 부분의 위치 다음 인덱스를 반환
*/
private int gallopRight(int key, int[] array, int base, int lenOfA) {
int lo = 0; // 이전 탐색(gallop) 지점
int hi = 1; // 현재 탐색(gallop) 지점
/*
* RUN B의 시작지점 값(key)이 RUN A의 시작지점 값보다 작을 경우
* 제외 될 원소는 없으므로 0 리턴
*/
if(key < array[base]) {
return 0;
}
else {
/*
gallopRight ->
RUN A key RUN B
______________________________ ______________________________
[ | | || | | |MAX] [MIN| | | | || | ]
------------------------------ ------------------------------
|___________| |______________| |___________________| |______|
less than MIN RUN A' RUN B' greater than MAX
|____________________________________|
merge RUN A' and RUN B'
*/
int maxLen = lenOfA; // galloping을 하여 가질 수 있는 최대 한계값
while (hi < maxLen && array[base + hi] <= key) {
lo = hi;
hi = (hi << 1) + 1;
if (hi <= 0) { // overflow 발생시 run A의 끝 점으로 초기화
hi = maxLen;
}
}
if (hi > maxLen) {
hi = maxLen;
}
}
lo++;
// binary search (Upper Bound)
while (lo < hi) {
int mid = lo + ((hi - lo) >>> 1);
if (key < array[base + mid]) {
hi = mid;
} else {
lo = mid + 1;
}
}
return hi;
}
/**
* gallop_left() 함수를 수행하여 RUN A 의 첫번째 원소(오른쪽 끝)보다
* 큰 원소들이 첫번째로 출현하는 위치를 RUN B 에서 찾는다.
*
*
* @param key run A의 key
* @param array 배열
* @param base run B의 시작 지점
* @param lenOfB run B 의 길이
* @return 제외되어야 할 부분의 위치 다음 인덱스를 반환
*/
private int gallopLeft(int key, int[] array, int base, int lenOfB) {
int lo = 0;
int hi = 1;
/*
* key가 B의 탐색의 첫 위치(오른쪽 끝)보다 크면 제외되어야 할 부분은 없으므로
* run B의 길이를 반환
*/
if (key > array[base + lenOfB - 1]) {
return lenOfB;
}
else {
/**
<- gallopLeft
RUN A RUN B
______________________________ ______________________________
[ | | || | | |MAX] [MIN| | | | || | ]
 ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄  ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄
|___________| |______________| |___________________| |______|
less than MIN RUN A' RUN B' greater than MAX
|____________________________________|
merge RUN A' and RUN B'
*/
// run B의 오른쪽부터 시작해야하므로 뒤쪽 시작점을 가리키는 변수
int startPointOfRun = base + lenOfB - 1;
int maxLen = lenOfB; // galloping을 하여 가질 수 있는 최대 한계값
while (hi < maxLen && key <= array[startPointOfRun - hi]) {
lo = hi;
hi = (hi << 1) + 1;
// overflow가 발생시 runB의 끝점(왼쪽 끝)으로 초기화
if (hi <= 0) {
hi = maxLen;
}
}
if (hi > maxLen) {
hi = maxLen;
}
/*
* 뒤에서부터 탐색했기 때문에 실제 가리키는 인덱스는 lo > hi 이므로
* 이분 탐색을 하기 위해 run B에 대해 가리키는 지점을 서로 바꿔준다.
*/
int temp = lo;
lo = lenOfB - 1 - hi;
hi = lenOfB - 1 - temp;
}
lo++;
// binary search (lower bound)
while (lo < hi) {
int mid = lo + ((hi - lo) >>> 1);
if (key <= array[base + mid]) {
hi = mid;
} else {
lo = mid + 1;
}
}
return hi;
}
/**
* 상대적으로 낮은 인덱스에 위치한 run을 기준으로 복사하여
* 실제 배열 원소를 병합하는 메소드
*
* @param start1 RUN A에서의 병합 시작 지점
* @param length1 RUN A에서의 병합해야 할 길이(개수)
* @param start2 RUN B에서의 병합 시작 지점
* @param length2 RUN B에서의 병합해야 할 길이(개수)
*/
private void mergeLo(int start1, int length1, int start2, int length2) {
// RUN A 를 담을 임시 복사 배열
int[] temp = new int[length1];
System.arraycopy(array, start1, temp, 0, length1); // RUN A를 temp 배열에 복사
int insertIdx = start1; // 재배치 되는 위치
int runBIdx = start2; // RUN B의 탐색 위치
int tempIdx = 0; // 복사한 RUN A의 탐색 위치
int leftRemain = length1; // 배치해야 할 RUN A의 원소 개수
int rightRemain = length2; // 배치해야 할 RUN B의 원소 개수
// 두 원소 중 먼저 소진 될 때 까지 반복
while (leftRemain != 0 && rightRemain != 0) {
// RUN B < RUN A 라면 RUN B 원소 삽입
if (array[runBIdx] < temp[tempIdx]) {
array[insertIdx++] = array[runBIdx++];
rightRemain--;
} else {
array[insertIdx++] = temp[tempIdx++];
leftRemain--;
}
}
// 왼쪽 부분 리스트가 남아있을 경우
if (leftRemain != 0) {
System.arraycopy(temp, tempIdx, array, insertIdx, leftRemain);
}
else { // 오른 쪽 부분 리스트가 남아있을 경우
System.arraycopy(array, runBIdx, array, insertIdx, rightRemain);
}
}
/**
* 상대적으로 높은 인덱스에 위치한 run을 기준으로 복사하여
* 실제 배열 원소를 병합하는 메소드
*
* @param start1 RUN A에서의 병합 시작 지점
* @param length1 RUN A에서의 병합해야 할 길이(개수)
* @param start2 RUN B에서의 병합 시작 지점
* @param length2 RUN B에서의 병합해야 할 길이(개수)
*/
private void mergeHi(int start1, int length1, int start2, int length2) {
// RUN B 를 담을 임시 복사 배열
int[] temp = new int[length2];
System.arraycopy(array, start2, temp, 0, length2);
int insertIdx = start2 + length2 - 1; // 재배치되는 위치
int runAIdx = start1 + length1 - 1; // run A의 탐색 위치
int tempIdx = length2 - 1; // 복사한 run B의 탐색 위치
int leftRemain = length1; // 배치해야 할 RUN A의 원소 개수
int rightRemain = length2; // 배치해야 할 RUN B의 원소 개수
while (leftRemain != 0 && rightRemain != 0) {
// RUN A' > RUN B' 라면 RUN A' 원소 삽입 (내림차순이기 때문)
if (array[runAIdx] > temp[tempIdx]) {
array[insertIdx--] = array[runAIdx--];
leftRemain--;
} else {
array[insertIdx--] = temp[tempIdx--];
rightRemain--;
}
}
// 오른쪽 부분 리스트가 남아있을 경우
if (rightRemain != 0) {
System.arraycopy(temp, 0, array, start1, rightRemain);
} else {
System.arraycopy(array, start1, array, start1, leftRemain);
}
}
} // IntMergeStack class
public static void sort(int[] a) {
sort(a, 0, a.length);
}
public static void sort(int[] a, int lo, int hi) {
int remain = hi - lo;
// 정렬해야 할 원소가 1개 이하일 경우 정렬 할 필요가 없다.
if(remain < 2) {
return;
}
/**
* 일정 크기 이하의 배열이라면
* binaryInsertionSort로 정렬 뒤 바로 반환
*
* @see BinaryInsertionSort.BinaryInsertionSort
*/
if(remain < THRESHOLD) {
int increaseRange = getAscending(a, lo, hi);
BinarySort(a, lo, hi, lo + increaseRange);
return;
}
IntMergeStack ims = new IntMergeStack(a);
int minRun = minRunLength(remain); // run의 최소 길이
do {
/*
* 정렬 된 구간의 길이를 구한다.
*/
int runLen = getAscending(a, lo, hi);
/*
* 만약 정렬 된 부분의 길이가 minRun 보다 작다면
* 정렬 된 부분 길이를 포함한 부분 배열에 대해
* 이진 삽입 정렬을 시행한다.
*/
if(runLen < minRun) {
/*
* [lo : lo+minRun] 구간에 대해 정렬
*
* counts : run에 있는 요소의 총 개수
* 이 때 최소 run 크기가 남은 원소 개수보다 클 수 있으므로 이를 처리해준다.
*/
int counts = remain < minRun ? remain : minRun;
/*
* BinarySort(array, lo, hi, start);
* index[lo] ~ index[lo + counts] 구간을 삽입 정렬을 하되,
* index[lo + runLen] 부터 삽입정렬을 시작함.
* (앞서 구한 오름차순 길이인 runLen에 의해 lo + runLen의 이전 인덱스는 이미 오름차순 상태임)
*/
BinarySort(a, lo, lo + counts, lo + runLen);
// 이진 삽입 정렬이 수행되었기에 증가하는 길이는 endPoint가 된다.
runLen = counts;
}
// stack에 run의 시작점과 해당 run의 길이를 스택에 push한다.
ims.pushRun(lo, runLen);
ims.merge();
lo += runLen;
remain -= runLen;
} while(remain != 0); // 정렬 해야 할 원소가 0개가 될 때 까지 반복
ims.mergeForce(); // 마지막으로 스택에 있던 run들 모두 병합
}
// ============ 아래는 Binary Insertion Sort에서 구현했던 내용들임 ================ //
private static void BinarySort(int[] a, int lo, int hi ,int start) {
if(lo == start) {
start++;
}
for (; start < hi; start++) {
int target = a[start];
int loc = binarySearch(a, target, lo, start);
int j = start - 1;
while (j >= loc) {
a[j + 1] = a[j];
j--;
}
a[loc] = target;
}
}
private static int binarySearch(int[] a, int key, int lo, int hi) {
int mid;
while (lo < hi) {
mid = (lo + hi) >>> 1;
if (key < a[mid]) {
hi = mid;
}
else {
lo = mid + 1;
}
}
return lo;
}
private static int getAscending(int[] a, int lo, int hi) {
int limit = lo + 1;
if (limit == hi) {
return 1;
}
if (a[lo] <= a[limit]) {
while (limit < hi && a[limit - 1] <= a[limit]) {
limit++;
}
}
else {
while (limit < hi && a[limit - 1] > a[limit]) {
limit++;
}
reversing(a, lo, limit);
}
return limit - lo;
}
private static void reversing(int[] a, int lo, int hi) {
hi--;
while (lo < hi) {
int temp = a[lo];
a[lo++] = a[hi];
a[hi--] = temp;
}
}
}
10. 카운팅 정렬(Counting Sort)
시간 복잡도가 매우 빠른 엄청난 성능을 보여주는 알고리즘

다음 과 같은 배열이 있다고 가정해 보자.
과정 1)
array를 한번 순회 하면서 각 값이 나올 때 마다 해당 값을 couting에 1씩 증가 시켜준다.

index 0~11 순으로 가면서 각 값이 나올때마다 값을 1씩 증가 시켜 counting에 저장한다.
과정 2)
배열의 각 값을 누적합으로 변환 시켜준다.
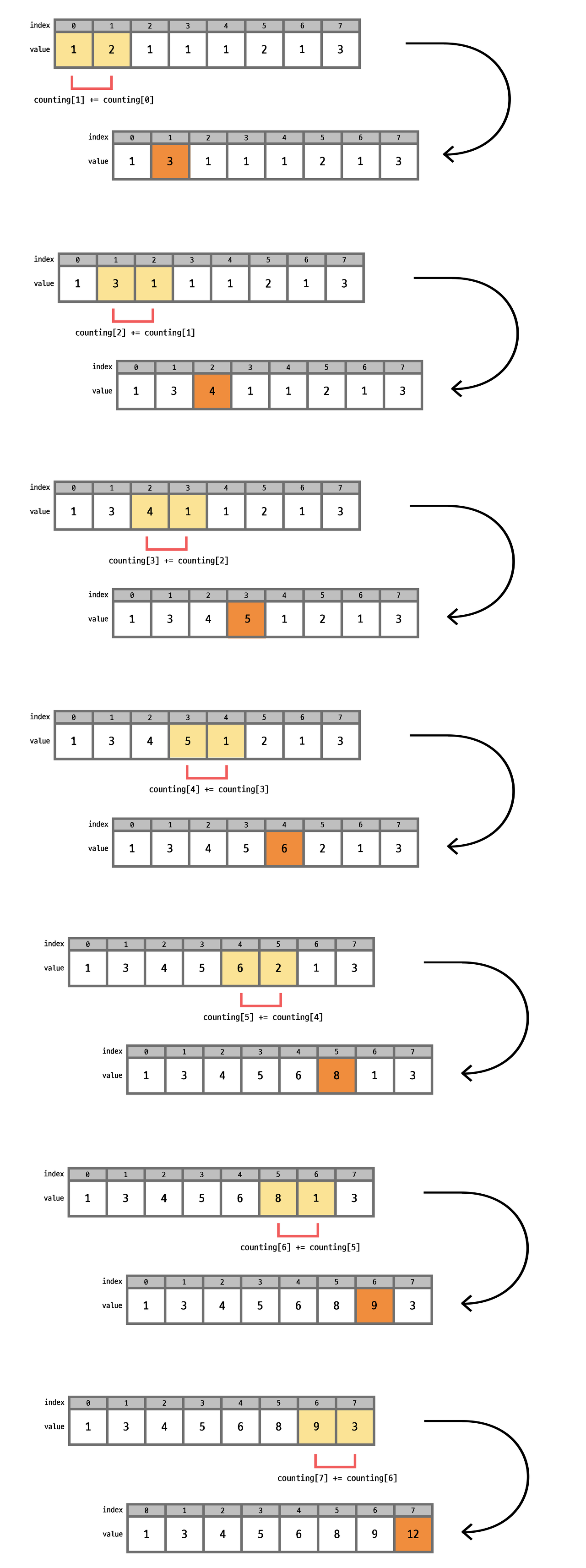

과정 3)
array[0] = 7 이다 이 valule를 counting[n] n에다가 넣어 주면 counting[7] = 12 이다. 여기서 12 - 1 = 11이 인덱스가 된다.
그러면 새로운 배열 result 의 index 11의 값은 7이 된다.
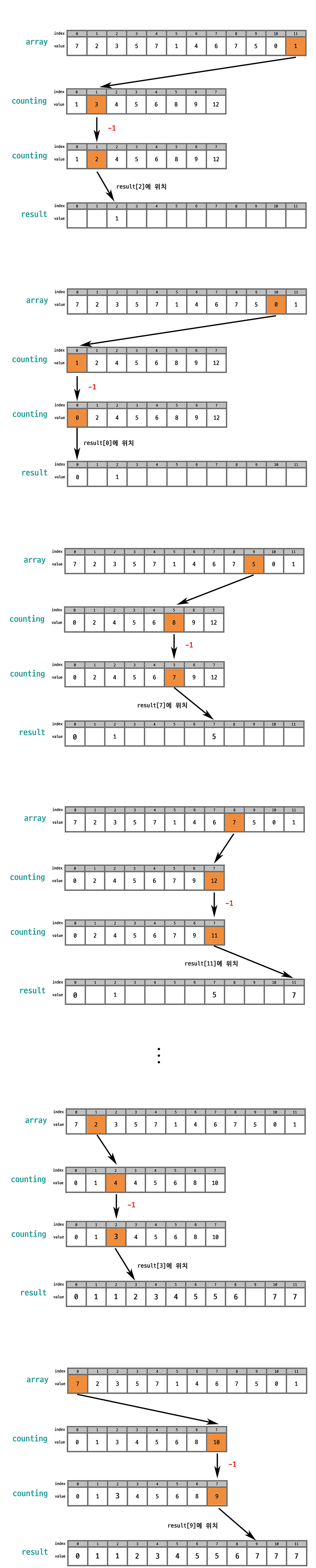
Counting Sort는 특정 타입에 한정되어 있고, 만약 입력되는 수의 개수는 적지만 ,수의 범위가 매우 클 경우 메모리 낭비가 심해 실생활에서는 쓰이지 않으나, 백준에서는 자주 쓰인다.
위 그림에 대한 코드는 아래와 같다.
public class CountingSort {
public static void main(String[] args) {
int[] array = new int[100]; // 수열의 원소 : 100개
int[] counting = new int[31]; // 수의 범위 : 0 ~ 30
int[] result = new int[100]; // 정렬 될 배열
for(int i = 0; i < array.length; i++) {
array[i] = (int)(Math.random()*31); // 0 ~ 30
}
// Counting Sort
// 과정 1
for(int i = 0; i < array.length; i++) {
// array 의 value 값을 index 로 하는 counting 배열 값 1 증가
counting[array[i]]++;
}
// 과정 2
for(int i = 1; i < counting.length; i++) {
// 누적 합 해주기
counting[i] += counting[i - 1];
}
// 과정 3
for(int i = array.length - 1; i >= 0; i--) {
/*
* i 번쨰 원소를 인덱스로 하는 counting 배열을 1 감소시킨 뒤
* counting 배열의 값을 인덱스로 하여 result에 value 값을 저장한다.
*/
int value = array[i];
counting[value]--;
result[counting[value]] = value;
}
/* 비교 출력 */
// 초기 배열
System.out.println("array[]");
for(int i = 0; i < array.length; i++) {
if(i % 10 == 0) System.out.println();
System.out.print(array[i] + "\t");
}
System.out.println("\n\n");
// Counting 배열
System.out.println("counting[]");
for(int i = 0; i < counting.length; i++) {
if(i % 10 == 0) System.out.println();
System.out.print(counting[i] + "\t");
}
System.out.println("\n\n");
// 정렬된 배열
System.out.println("result[]");
for(int i = 0; i < result.length; i++) {
if(i % 10 == 0) System.out.println();
System.out.print(result[i] + "\t");
}
System.out.println();
}
}
간단히 로직만 보면 아래와 같다.
public class counting_sort {
public static void main(String[] args) {
int[] arr = new int[101]; // 수의 범위 : 0 ~ 100
for (int i = 0; i < 50; i++) { // 수열의 크기 : 50
arr[(int) (Math.random() * 101)]++; // 0 ~ 100
}
for(int i = 0; i < arr.length; i++) {
while(arr[i]-- > 0) { // arr 값이 0보타 클 경우
System.out.print(i + " ");
}
}
}
}전체 정렬의 시간 복잡도
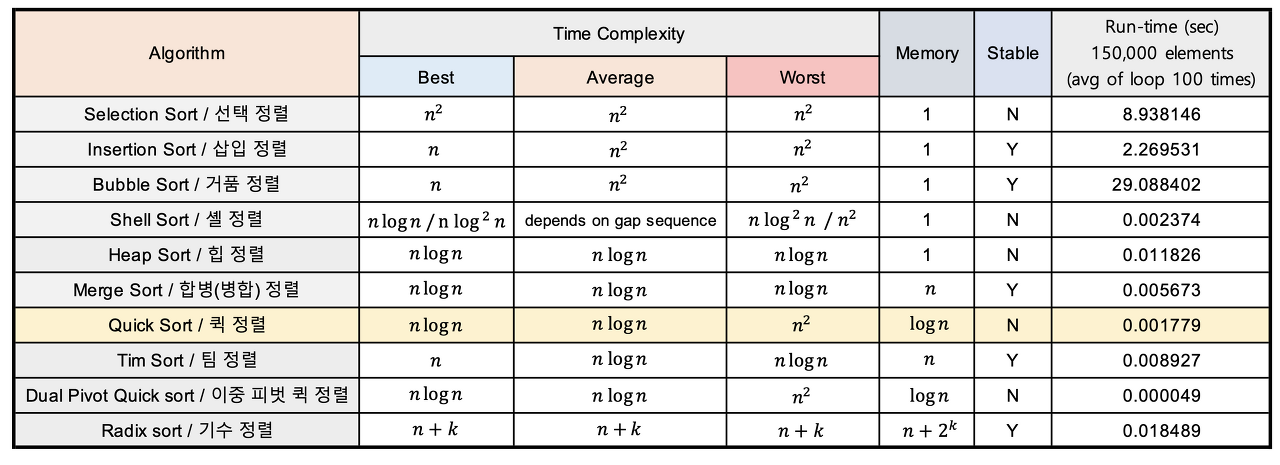
정말 간단하게 작성했다.
자세한 공부는 아래서 하자...
Stranger's LAB
코딩과 관련하여 다양한 알고리즘 문제를 풀어보고, 프로그래밍 언어를 이해해 볼 수 있도록 돕고자 만든 블로그 입니다.
st-lab.tistory.com
실 생활에서는 팀 정렬과 퀵 정렬이 많이 쓰인다. 적어도 퀵 정렬은 알고 있자..
'자료구조 || 알고리즘' 카테고리의 다른 글
| 트리와 전위,중위,후위 순회 (0) | 2022.06.11 |
|---|---|
| 스택(Stack)과 큐(Queue) (0) | 2022.06.11 |
| [자바] 문자열에서 사칙연산과 숫자 분리 (0) | 2022.06.09 |
| 브루트 포스(brute force) (0) | 2022.06.08 |
| 재귀함수 (0) | 2022.06.05 |


